HALMA

Humanlike Abstraction Learning Meets Affordance in Rapid Problem-Solving

The HALMA Game

Imagine you are in a dark space where you can see almost nothing. The only things you can see are colorful digits and some geometric symbols, as shown in this panel.

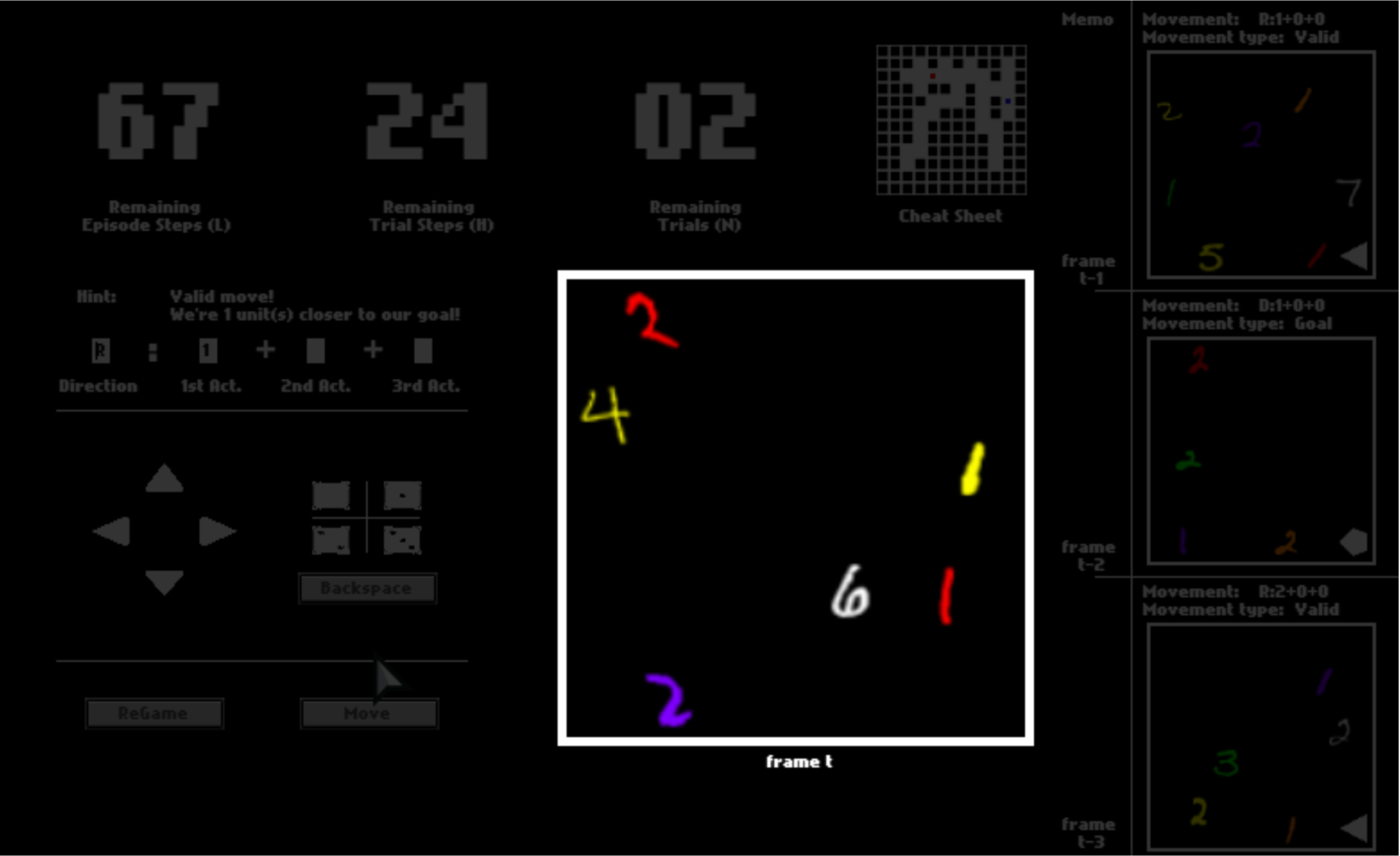
Meanwhile, you can make some moves to travel around the dark space. These moves are somehow “magical” because you may do a catapult-like instant transition after you make a decision. Specifically, every time you want to make a move, you first pick a direction from { , , , } and then a sequence of primitive actions from { , , , } with replacement. For example, you can pick for direction and + for the sequence of primitive actions.

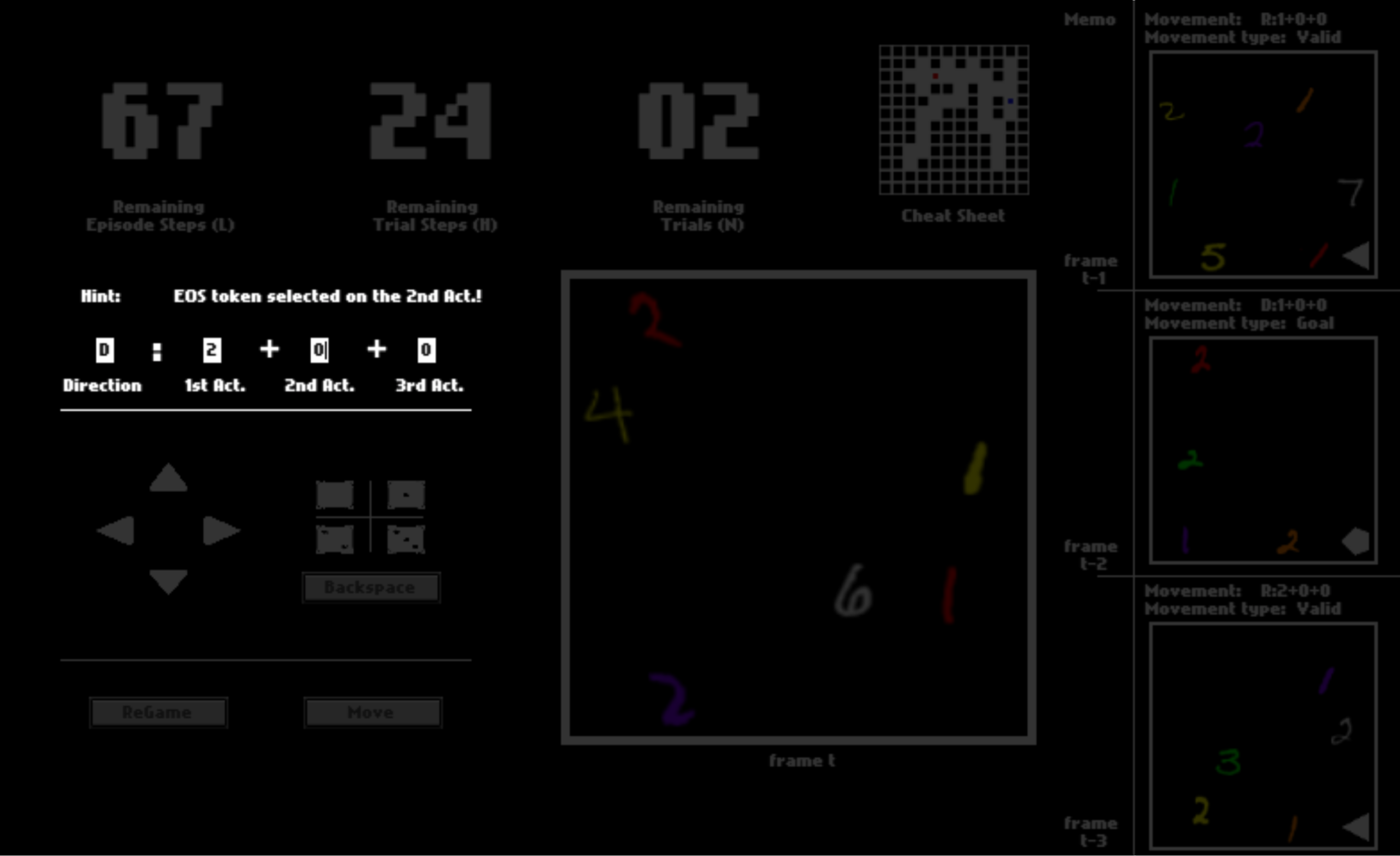
In the literature of Reinforcement Learning, such a sequence of actions is also dubbed an option (Sutton, 1999). Options may vary in their length. Here in this console, we constrain the maximum length of an option to be 3 (max_opt_len=3). Options do not have to be of the maximum length, thanks to the End of Sequence (EOS) token . That is, after you pick this token for a certain action in the sequence, all following actions will be automatically set to be .

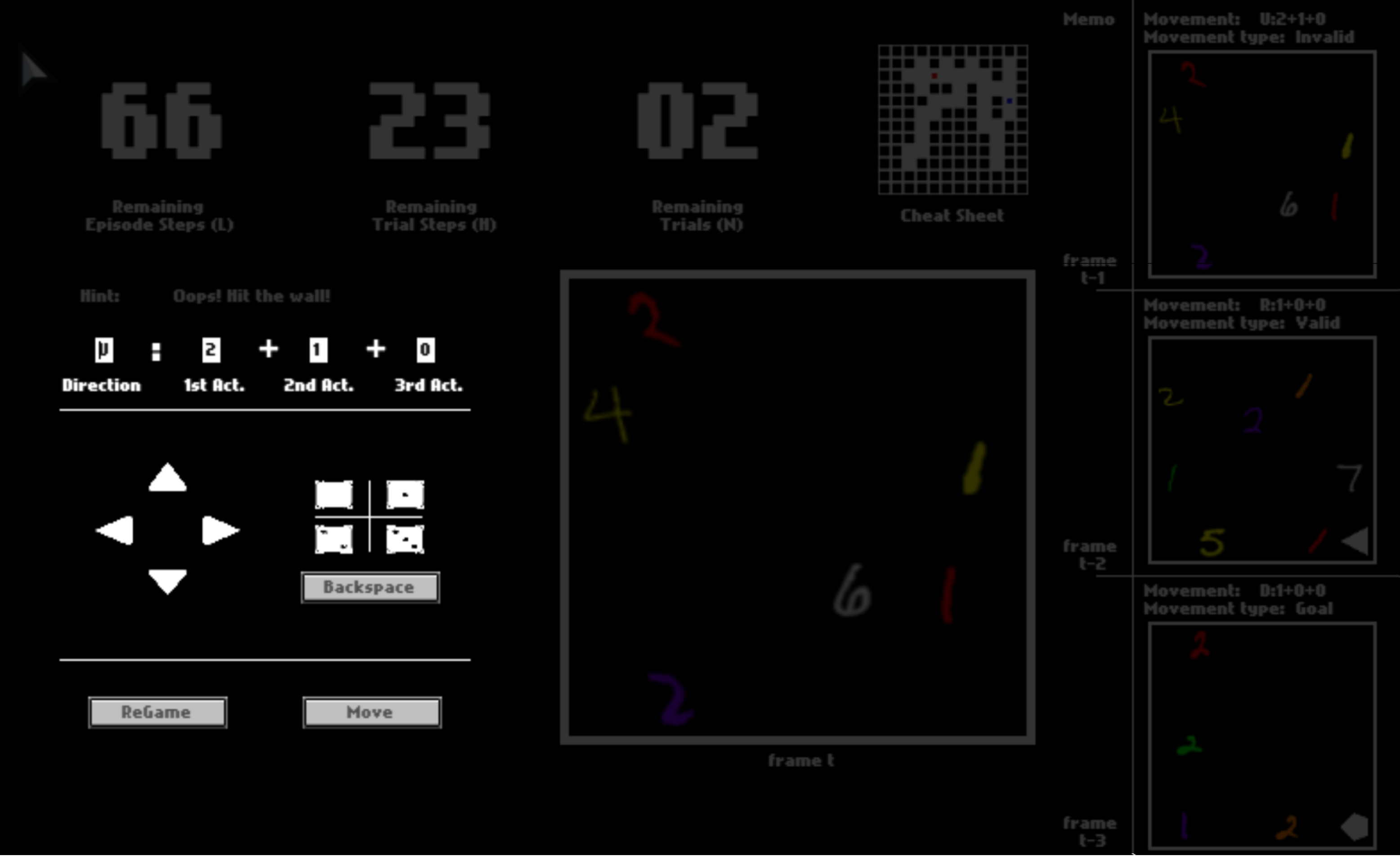
After you click “Move”, the option may or may not be executed, depending on whether it is valid (affordable) or not. If the move is executed, you will be catapulted to the next position. Otherwise, you will stay where you currently are.

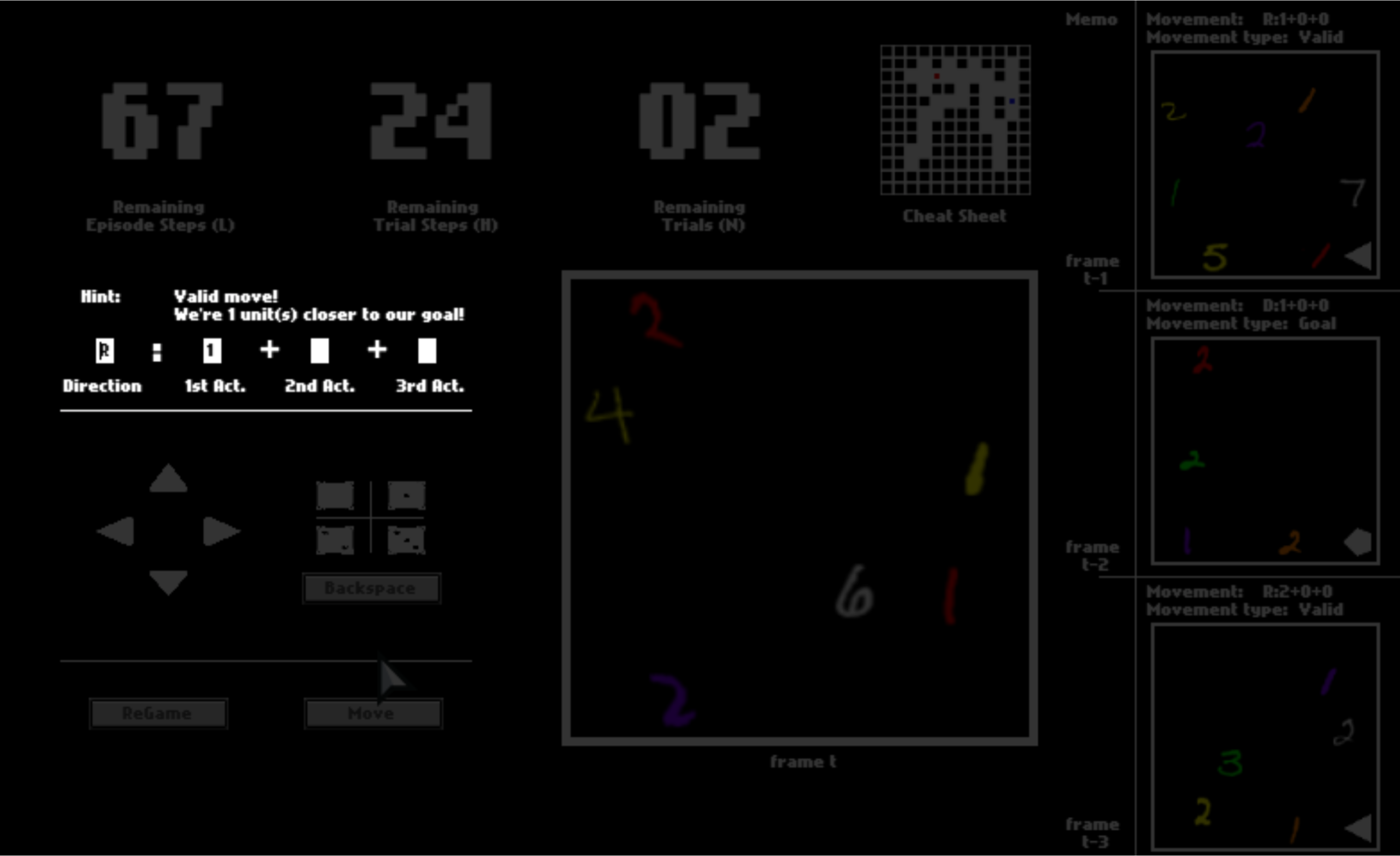
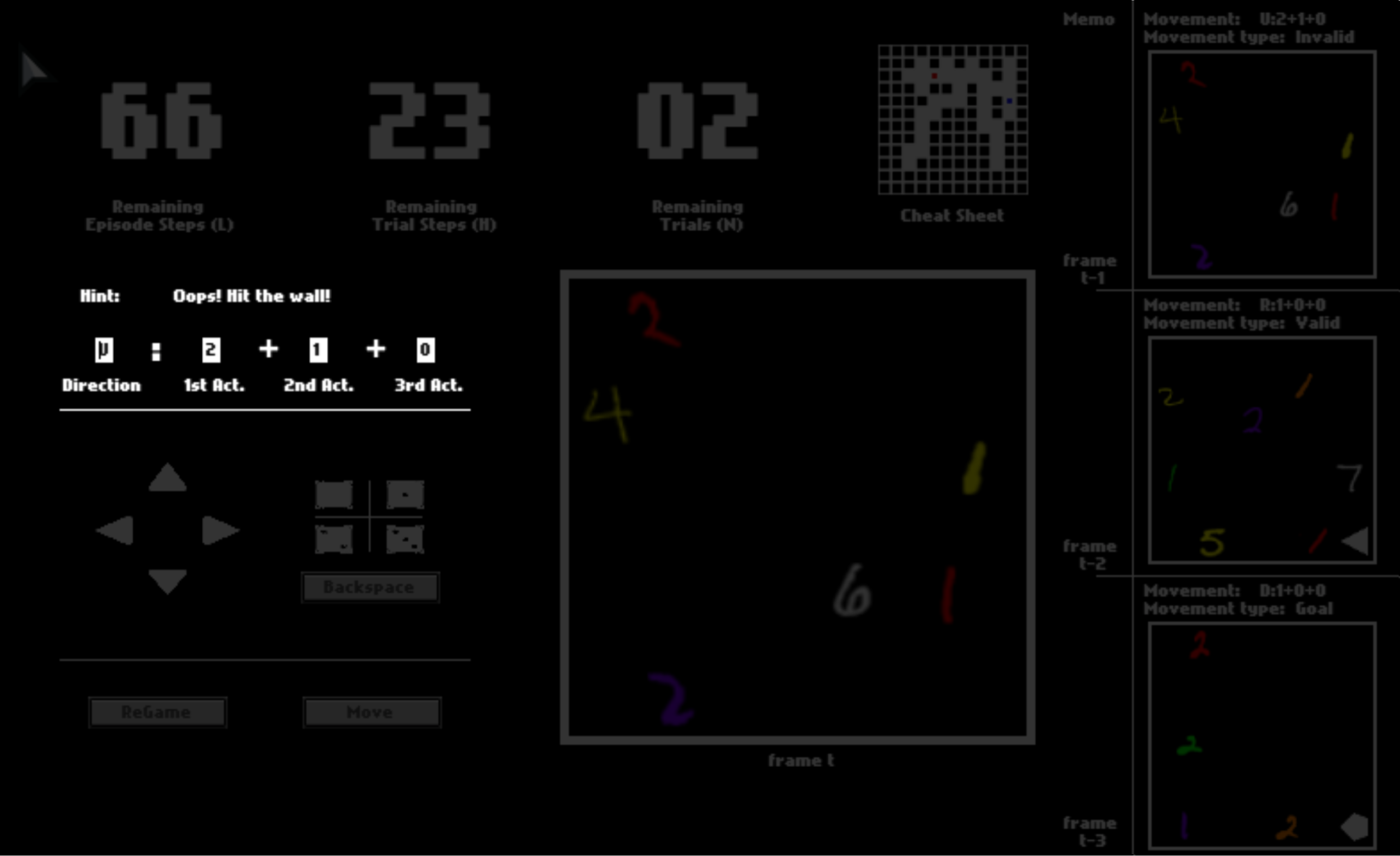
To help you memorize your previous panels and moves, your last three panels are presented to you. They may help you to understand this game while playing.

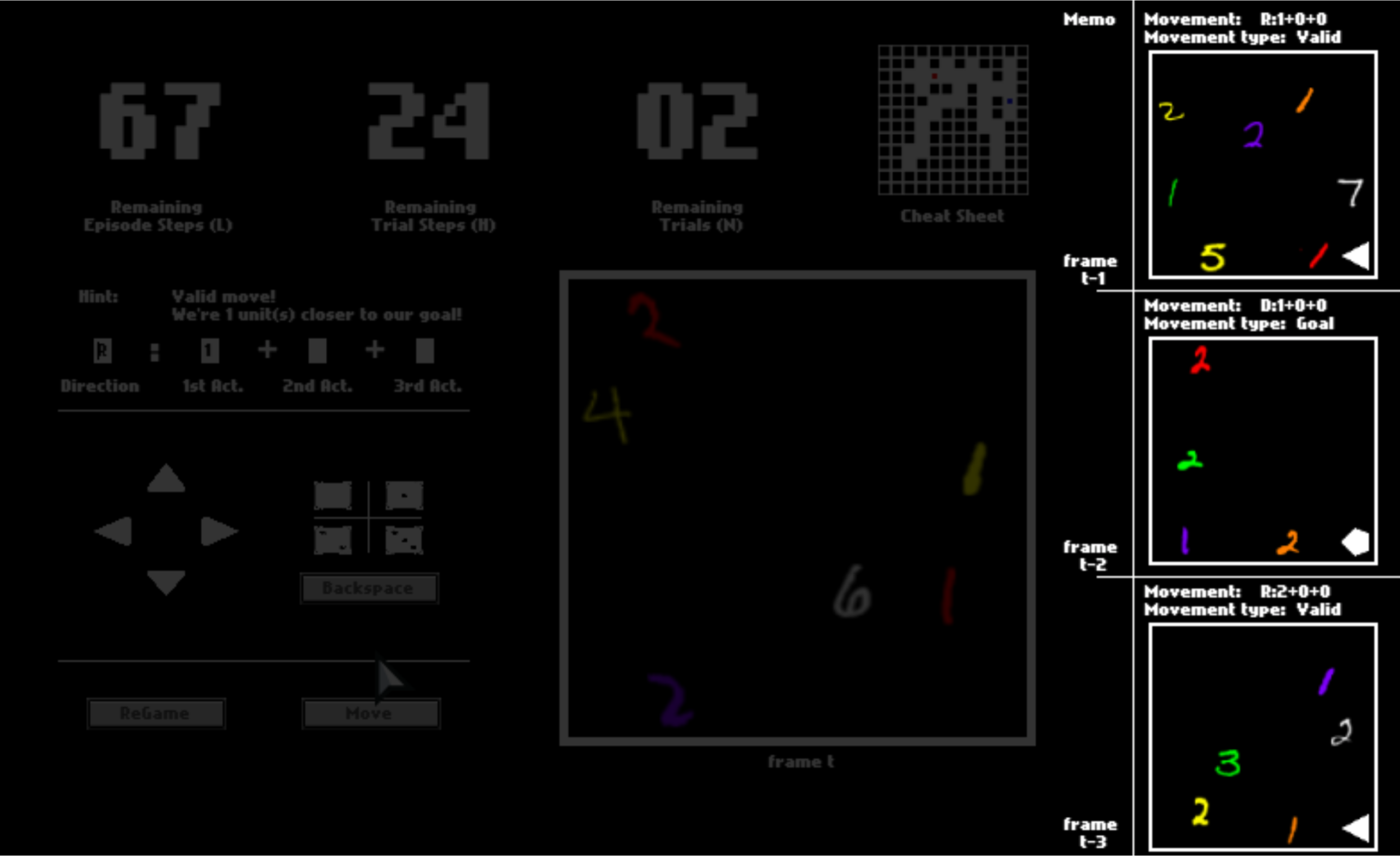
There are three numbers on the top, tracking the remaining number of steps in the current trial, the remaining number of trails, and the remaining number of steps in the current episode. You can equal “trials” in the HALMA game with “lives” in Atari games, and “episodes” with “levels”.

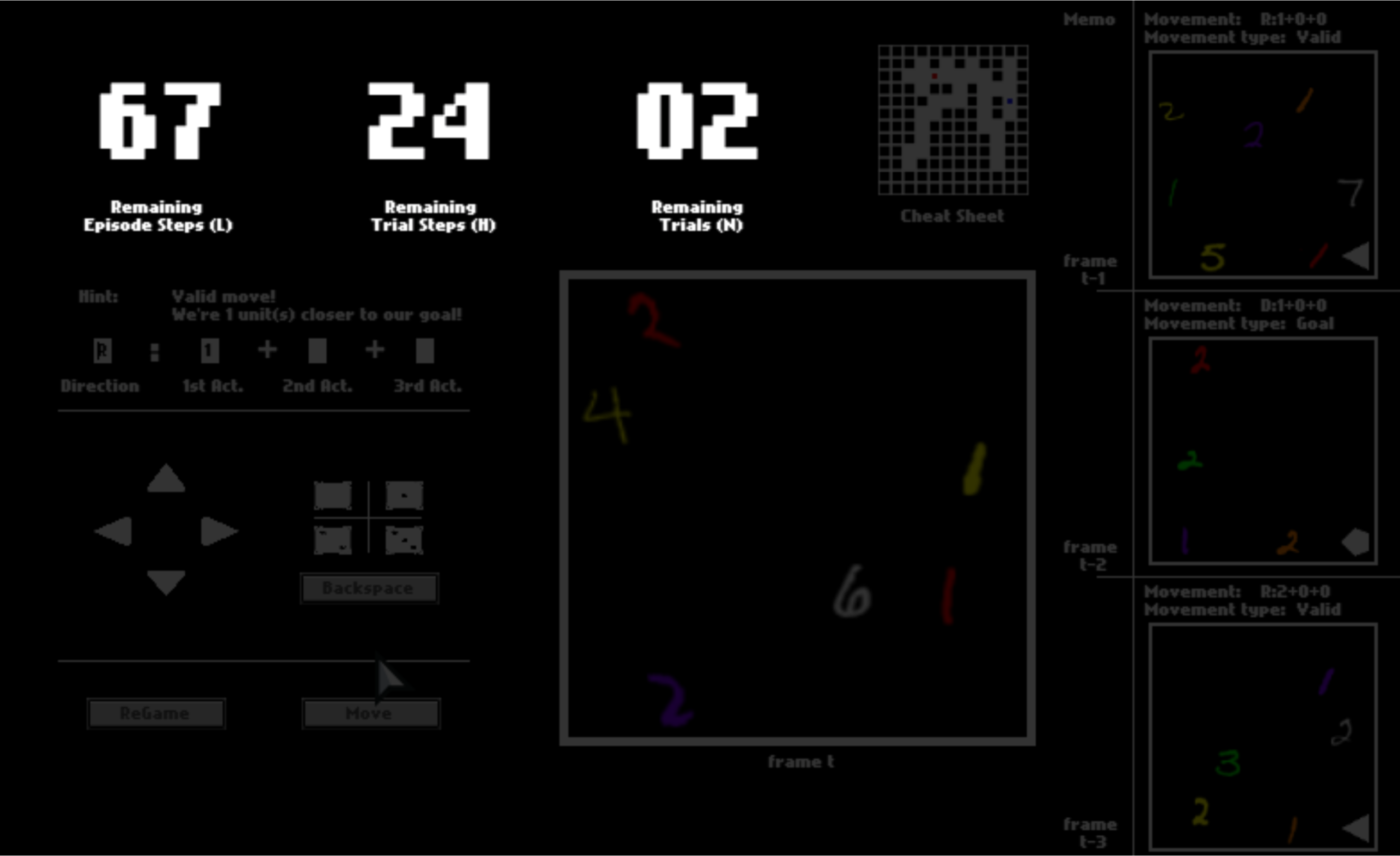
After one trial ends, you will be respawned to the initial position and start a new trial in the same space. You will have 3 trials in total. You will be scored by how fast you pass one trial, that is, how many steps you use on average.

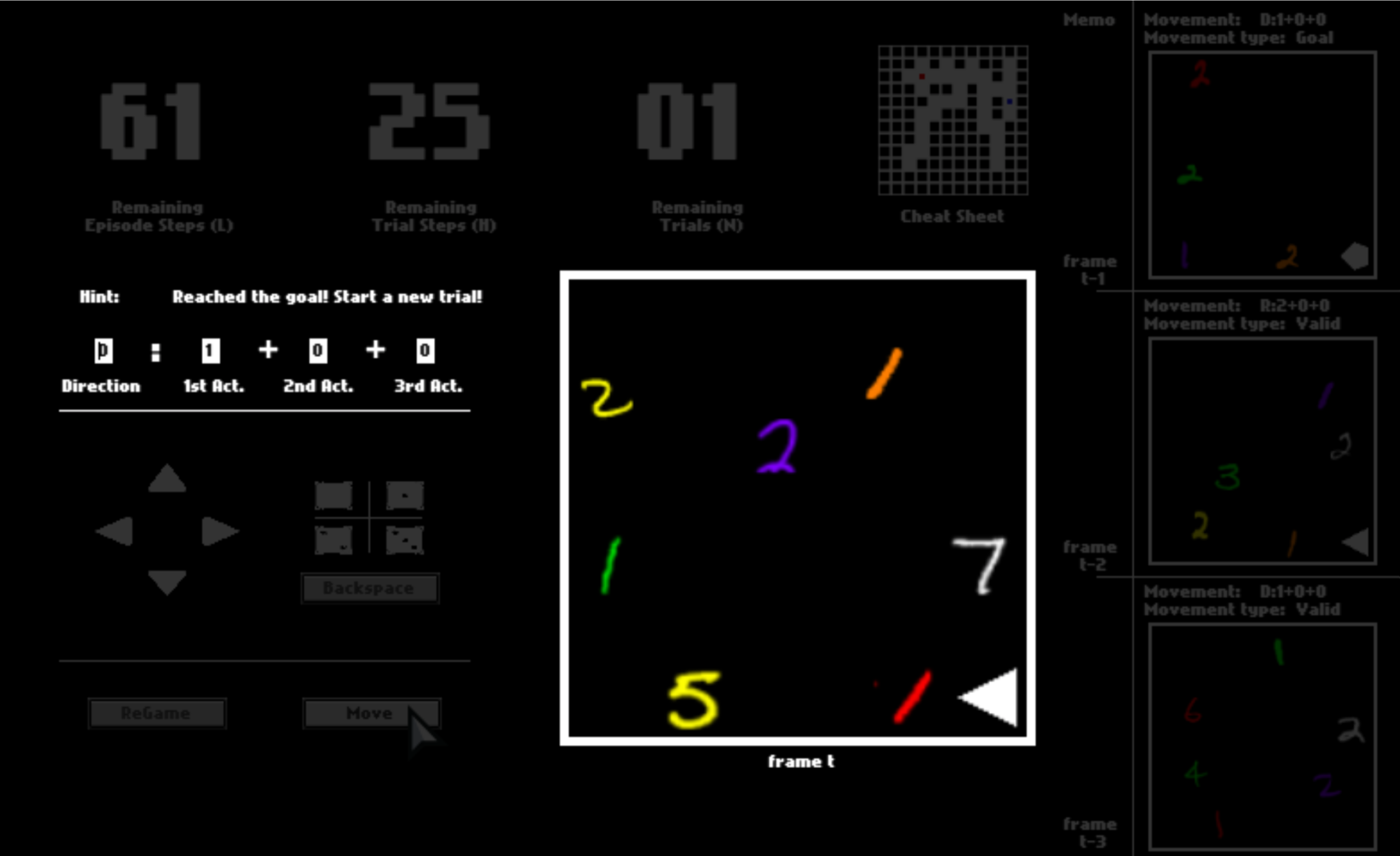
Even though you shall only see the panel as the observation in this game, to help you understand it faster, we enable a cheat sheet, which will be disabled in later episodes. This cheat sheet shows you about your surroundings, where you are, and where you go in the dark space.

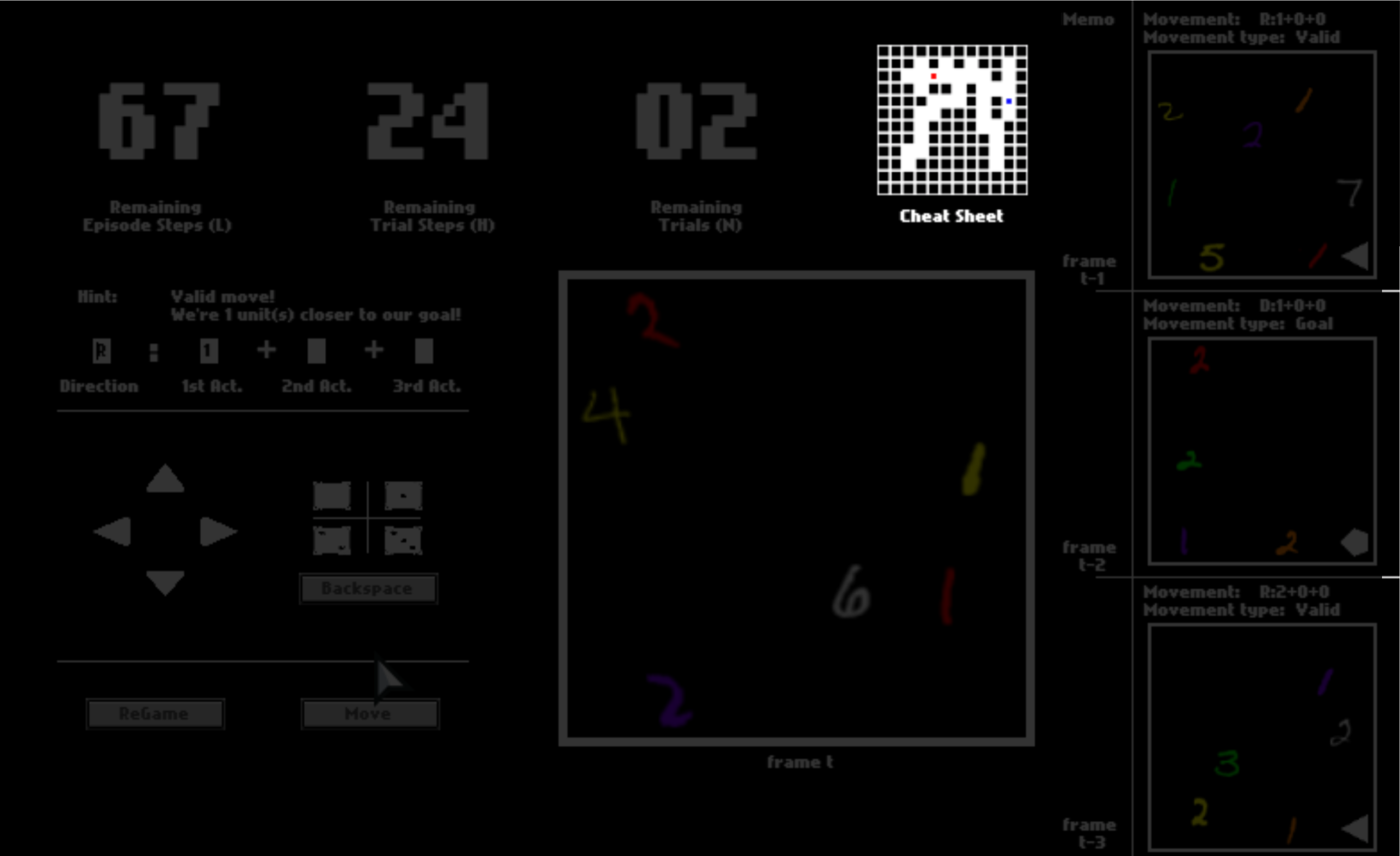
In your first episode, what you have to do is to dauntlessly explore the game space to figure out what the colorful digits and geometric symbols mean. The meaning of these symbols, that is, semantics, is consistent in all episodes. Henceforth, if you can figure out their meaning in this first episode with the help of the cheat sheet, you can probably solve all later episodes without the cheat sheet.

That’s all for the introduction of the HALMA game. Let’s start the first episode:

Find it challenging to understand the panels? Here is how we generate them.

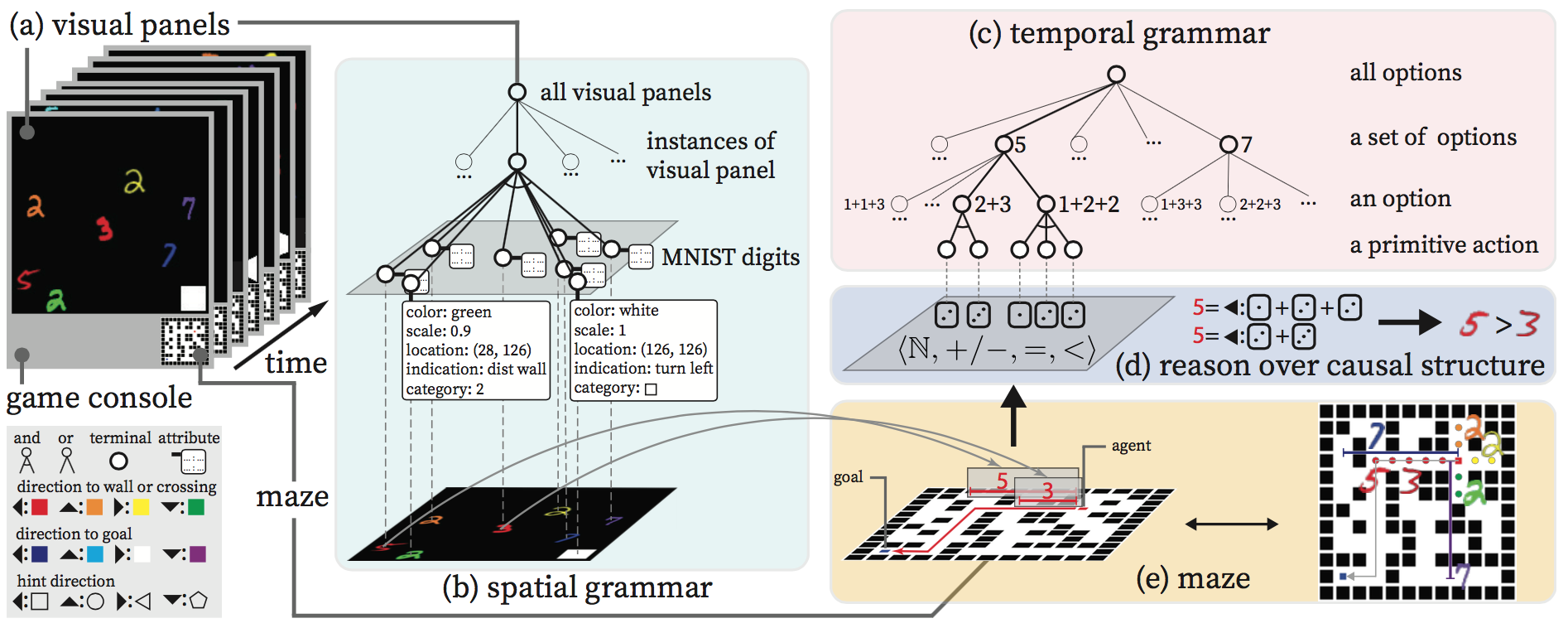
There are four colors -- red, orange, yellow, and green -- indicating left , up , right , down directions respectively for walls and crossings. For example, in Fig. 10, there is a red and a red : The smaller number, , indicates that the nearest crossing at the left direction is 3 units away, and the larger one, , indicates that the wall in the left direction is 5 units away. There are four other colors -- indigo, blue, white, purple -- indicating left , up , right , down directions respectively for the goal. So the correct interpretation of the panel in Fig. 10(a) is Fig. 10(e). Apart from these, there are also indications of those geometric symbols in the bottom right corner of the panels, which only appear when you stop at a crossing. These symbols are { , , , }, hinting you to go left , up , right , down respectively. These hints are pretty important, because missing them may lead you to dead ends where moving towards the goal direction may not lead you to the goal.

Now you can go back to play again. And remember that if you want to achieve high scores, you need to try your best to reach the goal as fast as possible. How would you play the first trial? How about the second and the third?

Check the following video for an oracle strategy in the first and the second trial.

In the second and the third trial, you should merge consecutive moves that are in the same direction into one move to save some timesteps.

Generalization Tests

Now that you have understood the concepts in this game, let’s test how you can generalize your understanding to a new maze. In this maze, you cannot see the cheat sheet anymore. Hence you have to count on your understanding of the panels.

Specifically, there are three levels of generalization: perceptual, conceptual, and algorithmic. Let’s check them one by one.

1. Perceptual generalization

In the new maze, you probably have seen some MNIST digits you haven’t seen in the previous episode. For example, the 5 in the previous episode is written as , but it is written as in this one. Nevertheless, you must have recognized it robustly when you are playing this new episode. Similarly, you haven’t seen a red 5 in the previous episode, but you can still recognize in the new episode. Moreover, you might have seen the panel in Fig. 8 in the previous episode, for which you need to compare and in the context of {,,,,,,}, but in this episode, you need to compare and in another context {,,,,,,}. It is quite remarkable that you, as a human, can generalize what you perceived previously to this new episode. We dub such a generalization perceptual generalization. And we coin tests to measure such capability semantic tests (ST).

Perceptual generalization characterizes agents’ capability to represent unseen perceptual signals. In his seminal book, Vision, Marr (1982) describes the process of vision as constructing a set of representations, parsing visual sensory data into descriptions. Learning an object-oriented representation of independent generative factors without supervision is thus believed to be a crucial precursor for the development of humanlike artificial intelligence.

2. Conceptual generalization

You probably have learned from our explanation for the first episode that the concepts of natural numbers and their arithmetics are important to understand the game of HALMA: between the two digits with the same colors, the lesser one is the distance to a crossing the larger one is the distance to a wall; the number of units to move in an option is the sum of all its constituting actions, which is also the difference between the digits for wall distance in the current frame and the next frame. Since you already know these concepts, you can simply retrieve your memory to bypass reasoning. But what if you have not learned these concepts yet? Imagine you were back to your preschool age, when you have not learned the formal concepts of natural numbers and arithmetics. After telling you 4 = 2 + 2, your teacher might quiz you with 4 ? 2. After telling you 3<4, 4<5, 3<5, 6<7, 7<8, your teacher might quiz you with 6 ? 8. You would have to do some preliminary mathematical reasoning to come up with their relations. Apparently, generalizing to unseen configurations like this is not challenging for humans, since most of us have become capable at the early age of school. Such a generalization requires a conceptual understanding of those abstract operations and relations. These relations are abstract because they are not perceivable through vision, and each of them is defined between a set of pairs rather than a specific pair. We dub such a generalization conceptual generalization. Since these tests may involve operations (+) over the action space and transitive reasoning over the relations (<), we coin tests to measure such capability affordance tests (AfT) and analogy tests (AnT).

While perceptual generalization closely interweaves with vision and control, conceptual generalization resides completely in cognition. The central challenge in conceptual generalization is: If there is a complete structure (also called pattern or regularity in abstract algebra (Grenander, 1993)) underlying the all possible instantiation of relations, how well can an agent perform in unseen scenarios after limited exposure to some instantiations? In plain English, it means the agent needs to understand what defines the abstract concepts such as add (+) and less than (<).

3. Algorithmic generalization

Even though different episodes may have different mazes, which hence afford different moves, once you understand those concepts, you know how to reconstruct mazes from the panels. However, since navigating in a maze is inherently partially observable, you still need to move smartly to assure you are reconstructing the right path to the goal, rather than wasting your time in deceptive branches. Fortunately, the HALMA game is designed to be easily solvable once you understand the concept space since there is a meta-strategy that is consistent in all mazes:

• If you are at the crossing, the agent should move towards the hinted direction;
• If you are not at the crossing, the agent should move towards the goal direction;
• The total number of units to move at each frame depends on the MNIST digits whose color aligns with the valid direction;
• If it is the first trial in a maze, you should stop at all crossings to obtain the hints;
• After the first trial, you should retrieve your memory for the whole trial, merge consecutive moves in the same direction and reach the goal faster.
As a human who understands the concept of natural numbers and arithmetics, you can always instantiate this meta-strategy into a concrete algorithm for an unseen maze problem. And hence as long as you understand HALMA, you can always achieve high scores in any mazes, no matter how it is different from the one you were trained with. We dub such a generalization algorithmic generalization. And it is measured with the average length of trials in some novel maze problems.

Algorithmic generalization describes the flexibility of building algorithms upon developed concepts in unseen problem instances in an understood domain. Specifically, for a problem domain where the internal structure contains an optimal exploration strategy, algorithmic generalization requires agents to discover this optimal strategy to explore efficiently. Furthermore, algorithmic generalization also measures the agent’s ability in long-term planning in unseen problems, after acquiring adequate information.

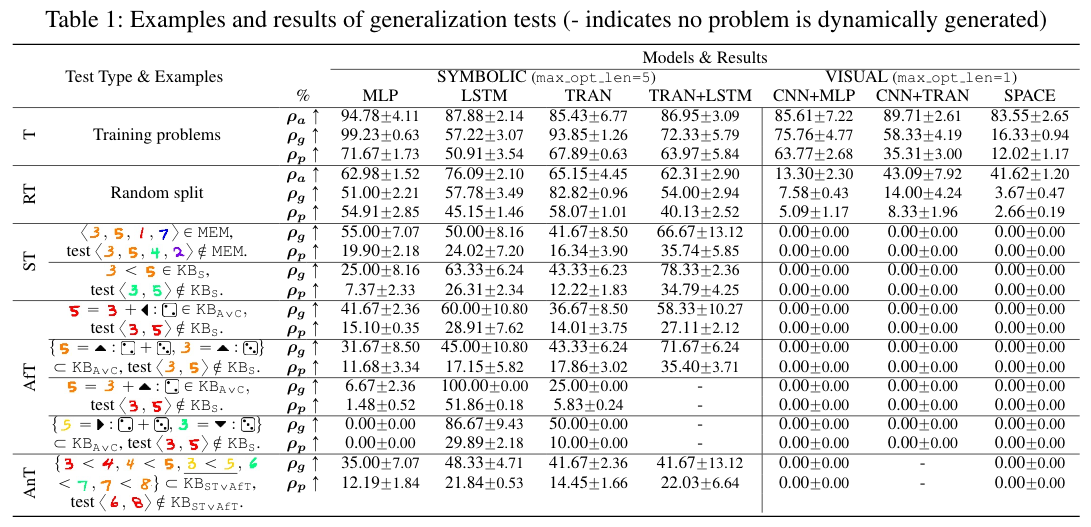
A humanlike agent should also pass these generalization tests. However, our experiments demonstrate the inefficacy of model-free reinforcement learning agents in concept development, abstract reasoning, and meta-learning. They fail to generalize their understanding, even when incorporated with generic inductive biases.

Towards this end, we would like to invite colleagues across the machine learning community to join our challenge.